Point de vue didactique, sommaire de la page
- Critères pour sélectionner les cartes
- Les particularités mathématiques du jeu du Chiffroscope
- Approfondissements didactiques sur la numération
Jouer au jeu du Chiffroscope doit permettre aux élèves d’apprendre le fonctionnement de la numération décimale. Les explications détaillées dans cette page doivent vous aider à mieux comprendre pourquoi et à quelles conditions cela marche.
1. Critères pour sélectionner les cartes
Pour que les parties de jeu soient productives pour les élèves en termes de stratégie et d’apprentissage, il faut que les tirages produisent des configurations intéressantes. Cela est partiellement contrôlable avec les sélections de cartes avec lesquelles jouent les élèves. Il est possible de sélectionner des cartes Nombre et des cartes Unité de numération d’une certaine façon pour que les parties amènent les élèves à travailler le principe de position, à s’interroger sur la place des zéros et à faire des conversions entre unités de numération.
Le choix du domaine numérique dépend du niveau de la classe, des objectifs et des besoins des élèves. Il correspond à des sélections de cartes Unité de numération associées à des cartes Nombre. Les sélections de cartes (numérotées U1 à U10 et N1 à N5 pour faciliter le repérage) ne précisent pas les niveaux de classe. Seuls figurent les domaines numériques abordés. C’est un choix pédagogique qui permet à chaque élève de travailler dans un domaine numérique adapté à ses compétences et non a priori dicté par le niveau scolaire de sa classe. Cela lui permet d’évoluer à son rythme sans ressentir de décalage par rapport aux attendus du niveau scolaire parfois inadaptés (trop simples ou trop difficiles). Ce choix est donc de nature à faciliter la différenciation au sein d’une même classe.
Ci-dessous, nous détaillons les sélections de cartes possibles et donnons des explications sur la façon de réaliser des sélections de cartes et de déterminer un nombre de tirages pour obtenir des parties de jeu intéressantes selon les aspects de la numération décimale de position qu’il faut travailler. Avec ces informations, vous pouvez vous aussi concevoir de nouvelles sélections de cartes Nombre et de cartes Unité de numération pour les adapter à vos objectifs spécifiques et aux besoins de vos élèves.
1.1. Sélections de cartes Unité de numération pour choisir le domaine numérique de travail
C’est avec la sélection de cartes Unité de numération que le domaine numérique est déterminé.
En plus du domaine numérique, le choix des unités de numération avec lesquelles travaillent les élèves permet de privilégier le principe de position ou le principe décimal. Si la sélection comporte une carte pour chaque unité de numération, les élèves ont peu de conversions à réaliser et travaillent plutôt sur le principe de position avec la gestion des zéros. Si la sélection comporte plusieurs cartes pour la même unité de numération, l’aléatoire du jeu conduit à ce qu’il y ait davantage de conversions, et donc favorise le travail du principe décimal. Cependant, l’aléatoire du jeu ne garantit pas que chaque partie amène les élèves à travailler systématiquement chaque principe. Le tableau ci-dessous récapitule les propositions qui sont détaillées plus bas, sélection par sélection.

Tous les fichiers pour l’impression des cartes sont disponibles dans la page Téléchargement.
Cartes Unité de numération Sélection 1 – U1 – Nombre cible < 99

Cette sélection ne contient que les unités et les dizaines, deux unités de numération différentes et adjacentes. Cette sélection est à privilégier pour l’étude des nombres inférieurs à 100 avec la sélection de cartes Nombre n°1. Associées à la sélection de cartes Nombre n°2, le tirage peut parfois conduire à un nombre cible à 3 chiffres.
Cartes Unité de numération Sélection 2 – U2 – Nombre cible < 999

Cette sélection propose trois unités de numération différentes et adjacentes. Elle permet d’écrire des nombres jusqu’aux milliers selon le tirage des cartes Nombre. Pour éviter des nombres cibles à 4 chiffres (aux milliers) tout en travaillant avec les cartes Nombre de 0 à 99, il faut retirer les cartes centaines de la sélection.
Cartes Unité de numération Sélection 3 – U3 – Nombre cible < 9 999

Cette sélection propose quatre unités de numération différentes et adjacentes. Elle permet d’écrire des nombres jusqu’aux dizaines de mille selon le tirage des cartes Nombre. Avec un tirage réduit à trois cartes, on favorise l’apparition de colonnes vides intercalées et donc la gestion des conversions (si nombres à 2 chiffres) ou des zéros.
Cartes Unité de numération Sélection 4 – U4 – Nombre cible < 9 999

Cette sélection propose trois unités de numération différentes et non adjacentes. Elle permet d’écrire des nombres jusqu’aux dizaines de mille selon le tirage des cartes Nombre. Quel que soit le tirage, il va conduire à écrire un nombre cible comportant un zéro au moins aux unités. Les centaines sont absentes du tirage. Selon le tirage, le chiffre des centaines du nombre cible sera un zéro ou bien résulte de la conversion des dizaines. Cette sélection permet d’aborder les points clefs de la numération avec gestion des zéros et des conversions, tout en travaillant avec des nombres relativement petits. Elle est adaptée pour le cycle 2 comme pour le cycle 3.
Cartes Unité de numération Sélection 5 – U5 – Nombre cible < 9 999 999

Cette sélection propose quatre unités de numération différentes, dont trois non adjacentes, pour travailler les grands nombres. Quel que soit le tirage, elle va conduire à écrire un nombre comportant au moins un zéro aux unités. Elle permet d’écrire des nombres cibles jusqu’aux dizaines de millions selon le tirage des cartes Nombre.
Les unités de numération nécessaires à l’écriture du nombre, bien qu’absentes du tirage (centaines et centaines de mille, peut être dizaines de millions), peuvent néanmoins avoir un chiffre différent de zéro, résultant d’une conversion de l’unité adjacente à droite. On peut favoriser le travail des zéros en choisissant de faire peu de tirages. Pour favoriser le travail des conversions, il faut aller jusqu’à cinq tirages. De façon générale, pour les nombres cibles assez grands, le nombre de tirages influence le type de stratégie à mettre en œuvre : trois tirages pour travailler les zéros, quatre ou cinq tirages pour travailler les conversions.
Cartes Unité de numération Sélection 6 – U6 – Nombre cible < 9 999 999

Cette sélection propose quatre unités de numération différentes et adjacentes pour travailler les grands nombres. Quel que soit le tirage, elle va conduire à écrire un nombre comportant des zéros aux unités, dizaines, centaines et unités de mille. Elle permet d’écrire des nombres jusqu’aux dizaines de millions selon le tirage des cartes Nombre. Les unités adjacentes devraient favoriser le recours aux conversions, plus ou moins faciles selon le tirage des cartes Nombre.
Cartes Unité de numération Sélection 7 – U7 – Nombre cible < 999 999 999

Cette sélection propose cinq unités de numération différentes dont trois adjacentes. Quel que soit le tirage, elle va conduire à écrire un nombre comportant des zéros aux unités et aux dizaines. Elle permet d’écrire des nombres jusqu’aux unités de milliards selon le tirage des cartes Nombre. Les unités de numération nécessaires à l’écriture du nombre mais absentes du tirage (unités de mille et dizaines de millions, éventuellement unités de milliards), peuvent avoir un chiffre différent de zéro selon le tirage des cartes Nombre dans les colonnes adjacentes et les conversions correspondantes.
Cartes Unité de numération Sélection 8 – U8 – Nombre cible < 999 999 999

Cette sélection propose les neuf unités de numération différentes et adjacentes nécessaires à l’écriture des nombres jusqu’aux centaines de millions, et selon le tirage des cartes Nombre, jusqu’aux unités de milliards. L’enseignant peut choisir de proposer aux élèves l’ensemble des cartes. Dans ce cas, il est probable que des unités intercalaires ne feront pas l’objet d’un tirage et conduiront à un zéro ou une conversion. Il peut aussi ne sélectionner que quelques unités adjacentes, favorisant les conversions entre ces unités adjacentes et l’usage de zéros intercalaires (entre deux chiffres différents de 0) ou en fin d’écriture du nombre. Il peut aussi choisir une sélection d’unités non adjacentes favorisant alors la gestion des zéros. Mais dans ce cas, il est probable que certaines conversions passent totalement inaperçues et viennent compléter des colonnes vides sans que l’élève en ait conscience.
Cartes Unité de numération Sélection 9 – U9 – Nombres décimaux

Cette sélection propose quatre unités de numération différentes et adjacentes. Elle permet d’écrire des nombres jusqu’aux centièmes et aux centaines selon le tirage des cartes Nombre. Avec cette sélection, les élèves ne peuvent plus utiliser si facilement la stratégie de retour à l’unité (FAQ et page « Stratégies et erreurs des élèves« ), stratégie couramment pratiquée avec les nombres entiers. Les élèves doivent trouver d’autres stratégies pour résoudre le problème et se référer à d’autres unités de numération.
Cartes Unité de numération Sélection 10 – U10 – Nombres décimaux

Cette sélection propose trois unités de numération différentes et non adjacentes. Les cartes unités simples et centièmes sont absentes. Le chiffre à indiquer aux unités simples sera soit un zéro soit le résultat d’une conversion provenant des dixièmes. De même le chiffre à indiquer aux centièmes sera soit un zéro soit le résultat d’une conversion provenant des millièmes. Selon les cartes Nombre choisies, cette sélection permet de travailler la conversion entre les dixièmes et les unités simples. Très souvent, les élèves séparent la partie entière de la partie décimale et ont beaucoup de difficulté à considérer ces deux parties en relation, et pas simplement juxtaposées, pour obtenir le nombre. Cela s’observe notamment lorsque les élèves ne réalisent pas les conversions nécessaires entre les dixièmes et les unités simples. Cette sélection peut contraindre les élèves à réaliser des conversions entre des unités de numération absentes du tirage, dont les unités simples. De plus, la question de la place de la virgule se posera pour écrire le nombre en dehors du tableau.
Lien vers les cartes Unité de numération sur la page Téléchargement.
1.2. Sélections de cartes Nombre pour aborder ou pas les conversions
Nous proposons cinq sélections de cartes Nombre contenant pour certaines uniquement des nombres à 1 chiffre (N1 et N2) et pour d’autres des nombres à 1 ou 2 chiffres (N3, N4 et N5). Nous expliquons les conséquences sur les types de tirages et les stratégies qui peuvent être privilégiées pour vous permettre de constituer d’autres sélections. Il y a 9 cartes par sélection pour optimiser l’impression (9 cartes par feuille A4) et non pour des raisons didactiques.

Cartes Nombre Sélection n°1

Cette sélection de nombres est la plus simple possible, car elle évite a priori les conversions entre unités de numération. En effet, même si deux ou trois cartes se trouvent dans la même unité de numération, le total n’excède pas 9 sauf exception. Elle n’aborde que peu d’éléments intéressants dans le jeu. Cependant, elle est utile pour les CP, au tout début.
Cartes Nombre Sélection n°2

Avec plusieurs cartes plus grandes que 5, le total des cartes Nombre tirées dans une même unité de numération peut être supérieur à 9. Le tirage conduit alors à effectuer une conversion entre deux unités de numération. Le fait d’aborder les conversions avec les élèves est un point important du jeu. Néanmoins, si, dans un 1er temps, vous souhaitez éviter ce cas tout en travaillant avec les nombres cibles de 0 à 99, il faut retirer les quatre cartes 6-7-7-8 de la sélection et faire jouer les élèves avec un tirage de 3 cartes associées aux unités de numération unités et dizaines.
Cartes Nombre Sélection n°3

Cette sélection introduit des nombres à deux chiffres. Elle offre la possibilité d’un tirage nécessitant des conversions, mais avec une probabilité réduite qui ne devrait pas apparaître à chaque partie. De même les conversions en cascades sont réduites. Elle n’est pas très pertinente pour travailler les grands nombres, sauf pour apprendre à gérer les zéros dans l’écriture d’un nombre et ainsi travailler le principe de position.
Cartes Nombre Sélection n°4

Cette sélection de cartes Nombre propose des nombres à un chiffre proches de 10 et des nombres à deux chiffres qui entrainent le passage à la dizaine supérieure lorsque plusieurs cartes sont tirées pour une même unité de numération. Avec ces nombres, l’addition au sein d’une unité de numération aboutie souvent à la nécessité d’une conversion.
Cartes Nombre Sélection n°5

L’intérêt de cette sélection est qu’elle permet de travailler des grands nombres cibles tout en nécessitant une stratégie de conversion. Elle peut cependant conduire à des conversions en cascade, notamment si le nombre cible n’est pas très grand. Elle ne doit pas être proposée aux élèves en première découverte. Elle s’avère pertinente seulement une fois qu’ils ont pu travailler et discuter des conversions. Cette sélection de cartes Nombre est plus intéressante à utiliser pour travailler les nombres à plus de 5 chiffres (donc associée avec les sélections U5, U6, U7 et U8), afin qu’il y ait besoin de faire des conversions et d’utiliser des zéros. Avec des nombres cibles à seulement 3 ou 4 chiffres, le travail devient plus technique et très calculatoire. Cela peut intéresser des élèves qui ont besoin d’aller plus loin et de développer leur expertise, mais ce n’est pas un objectif d’apprentissage.
Exemple de traitement technique lorsqu’il y a peu d’unités de numération, avec 4 tirages (45d, 28c, 19c et 67d) :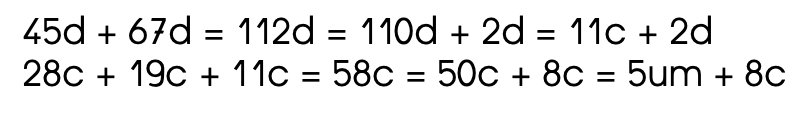
Le nombre s’écrit 5 820 suite à de nombreuses additions et conversions.
Lien vers les cartes Nombre sur la page Téléchargement.
1.3. Combiner les sélections de cartes Unité de numération et cartes Nombre
Le tableau présente les associations possibles entre les sélections de cartes Unité de numération et cartes Nombre pour travailler de préférence l’un ou l’autre des deux principes de la numération.

Sélections de cartes pour travailler prioritairement le principe de position
Pour travailler prioritairement le principe de position, il faut que l’élève se pose la question de faire apparaitre les chiffres à la bonne place dans le nombre en utilisant les zéros nécessaires. Pour cela :
- Choisir des cartes-nombres avec uniquement des nombres à 1 chiffre inférieurs à 5 (par exemple la sélection N1 ou une partie de N2 )
- Choisir peu d’unités de numération différentes (3 ou 4 maximum) qu’elles soient contiguës ou pas
- Pendant la partie de jeu, restreindre le nombre de tirages à 2 ou 3 (un tirage = une carte Nombre associée à une carte Unité de numération)
- Si utilisation de toutes les cartes Nombre des sélections N1 ou N2, présence de 6, 7 et 8, alors des conversions relativement faciles peuvent apparaître.
- Enlever des unités de numération pour faire apparaître des trous c’est-à-dire des unités de numération non contigües et avoir autant de cartes Nombre à 1 chiffre que d’unités de numération différentes.
Sélection de cartes pour travailler prioritairement le principe décimal
Pour travailler prioritairement le principe de décimal, il faut que l’élève rencontre la nécessiter de convertir entre deux unités de numération, adjacentes ou pas. Une façon de le provoquer consiste à avoir un nombre plus grand que 9 dans une colonne, grâce à une carte ou plusieurs cartes Nombre associées à une unité de numération. Pour cela :
- Choisir des cartes Nombre à 1 chiffre (sélection N1 ou N2) et
- Utiliser deux unités de numération contiguës
- Pendant la partie, faire 4 ou 5 tirages pour favoriser l’addition dans une même unité de numération
- Avec toutes les cartes N1, des conversions relativement faciles peuvent apparaître.
- Choisir les sélections de cartes Nombre N2 ou N3 et des cartes Unité de numération non contigües (U4, U5 ou U7 par exemple) : les conversions prendront le pas sur le travail de la position.
- Avec les sélections de cartes Nombre N2, N3, N4 et N5, les conversions prendront le pas sur la position surtout dans le cas d’une partie de jeu à 5 tirages (un tirage = une carte Nombre associée à une carte Unité de numération).
Partie facile, partie difficile, niveau de classe
Les parties sont a priori plus faciles avec des cartes Nombre à 1 chiffre et plus difficiles avec des cartes Nombre à 2 chiffres car elles amènent à traiter la question des nombres à 2 chiffres dans une colonne du tableau de numération. Mais c’est un peu plus complexe, car cela dépend aussi du nombre de tirages (variant de 3 à 5) et de la sélection des unités des numération. La difficulté d’une partie résulte au final des éléments suivants, bien que la dimension aléatoire du jeu ne permette pas de certifier le niveau de difficulté d’une partie :
- des nombres sur les cartes Nombre : les nombres à 1 chiffre pour les parties faciles, les nombres à 2 chiffres pour les parties difficiles ;
- des unités de numération : des unités de numération non adjacentes pour des parties faciles et peu d’unités de numération différentes et adjacentes pour des parties plus difficiles
- du nombre de tirages : avec trois tirages vous obtenez des parties faciles, avec 4 ou 5 tirages vous obtenez des parties plus difficiles.
Puisque l’aléatoire du jeu ne permet pas de contrôler complètement le niveau de difficulté des parties, les Arrêts sur image sont le moyen de proposer aux élèves des parties bien adaptées à vos objectifs. Par ailleurs, les niveaux de classe ne sont pas indiqués. Seuls les domaines numériques travaillés sont précisés et vous permettent de proposer à vos élèves des situations et des contextes numériques adaptés à leurs besoins, sans stigmatisation liée à un niveau de classe différent du leur.
2. Les particularités mathématiques du jeu du Chiffroscope
2.1. Écriture dans le tableau, écriture hors du tableau
Il faut clairement distinguer ce qui relève des écritures d’un nombre dans un tableau de numération de celles réalisées en dehors du tableau de numération. Les règles qui s’appliquent ne sont pas les mêmes.
Dans un tableau de numération, chaque valeur placée dans une colonne correspond explicitement à une unité de numération. Lorsqu’on extrait le nombre pour l’écrire hors du tableau de numération, il n’y a de la place que pour un seul chiffre de façon à ce qu’il soit explicitement affecté à une unité de numération. Ce qui était possible dans le tableau de numération ne l’est alors plus en dehors. Par exemple, dans le tableau de numération, on peut indiquer 23 dans la colonne des unités de mille et cela signifie sans ambiguïté 23 unités de mille. Mais en dehors du tableau, pour signifier les 23 unités de mille, il faut écrire obligatoirement 23 000. C’est-à-dire positionner le 2 immédiatement à gauche du 3 pour signifier les dizaines de mille et des zéros pour les centaines, dizaines et unités.
Dans l’image ci-dessous, le tirage 23 unités de mille, 50 centaines et encore 11 centaines, puis 45 unités et 8 unités désigne sans ambiguïté le nombre égal à 23 unités de mille, 61 centaines et 53 unités. Les cartes dans le tableau mettent clairement en correspondance le nombre (50 + 11 = 61) avec l’unité de numération centaine et le nombre (45 + 8 = 53) avec les unités. Cependant, si l’on extrait la suite de chiffres 23 61 0 53 en les juxtaposant hors du tableau de numération pour écrire le nombre correspondant, il n’est plus possible de savoir quel chiffre correspond à quelle unité de numération. L’écriture 2361053 ne correspond pas au nombre égal à 23 unités de mille, 61 centaines et 53 unités.

Figure 3- situation cartes N5 et U3. Plusieurs cartes de nombres à 2 chiffres dans une même colonne, avec conversion. Des colonnes non nommées (dizaines et dizaines de mille) à prendre en compte pour écrire le nombre : faut il utiliser des zéros ? ou bien le résultat des conversions fournira un chiffre dans ces colonnes ?
Pour pouvoir écrire le nombre en dehors du tableau, il faut respecter les principes de l’écriture décimale de position et donc utiliser des zéros et faire des conversions. Ces principes sont au cœur des stratégies gagnantes du jeu du Chiffroscope.
2.2. Le plateau de jeu
Le plateau de jeu présente un tableau aux colonnes sans nom prédéfini de format A4 en portrait. Les dimensions des feuilles autorisent leur placement sur une table classique d’élèves telle qu’on les rencontre assez fréquemment. Chaque feuille comporte 3 colonnes complètes et 2 demi-colonnes de chaque côté. La largeur des colonnes correspond aux dimensions des cartes Nombre et des cartes Unité de numération. Les demi-colonnes au bord de chaque feuille peuvent être assemblées bord à bord et constituer une colonne entière pour agrandir le plateau, aussi bien à gauche qu’à droite.

Il est nécessaire de laisser à la disposition des élèves un nombre suffisant d’exemplaires de ce plateau 3 + 2 ½colonnes. En effet, il est important qu’ils puissent décider eux-mêmes de le prolonger à gauche comme à droite, autant que nécessaire, selon leurs besoins au cours du jeu.
Au cours du jeu, ce plateau figure un tableau de numération un peu particulier : ‘ »le tableau flottant ».
2.3. Le tableau flottant
Le tableau de numération ne constitue pas un but d’apprentissage en soi. Il doit rester un outil pour aider les élèves à écrire les nombres et à réaliser des conversions. Il n’est pas nécessaire de le figer, en le présentant toujours de la même manière, comme on le voit couramment dans les manuels et pratiques de beaucoup d’enseignants. Ces configurations figées et stéréotypées, avec les unités simples toujours dans la dernière colonne à droite pour les entiers et un tableau fermé et limité aux strictes unités de numération nécessaires, laissent penser aux élèves que ce tableau ne peut pas être différent ni adapté au problème en cours. Lorsque l’enseignant donne systématiquement le tableau tout prêt, il prend en charge ces choix mathématiques et empêche l’élève d’y accéder.
Ainsi, le plateau papier du Chiffroscope est un tableau en plusieurs morceaux, dont les colonnes ne sont pas étiquetées. dans l’objectif d’amener les élèves à construire leur propre tableau afin de disposer du nombre de colonnes nécessaires au dépôt des cartes et à l’écriture du nombre. Cela permet de faire apparaître le tableau de numération comme un outil au service de l’élève et pas comme un nouvel objet à apprendre.
Pour cela, le tableau flottant a plusieurs particularités.
- Contrairement à un tableau de numération habituel dont les colonnes sont déjà nommées, le tableau flottant du Chiffroscope a des colonnes sans étiquette. Un tableau sans colonnes pré-étiquetées par les unités de numération rend nécessaire le remplissage par l’élève des en-têtes de colonne avec les unités de numération et permet de lui faire apprendre l’ordre des unités de numération, donc de travailler le principe de position.
- Il peut avoir trop de colonnes ou pas assez, à gauche ou à droite, c’est à l’élève de sélectionner les colonnes utiles et d’en ajouter si nécessaire. Ainsi l’élève organise le tableau selon ce dont il a besoin, transformant le tableau en outil.
- Les unités simples ne sont pas toujours placées dans la dernière colonne à droite pour habituer l’élève à ne pas être gêné par la présence de colonnes inutiles à gauche et à droite et le conduire à envisager qu’elles seront nécessaires pour d’autres nombres.
Au cours d’une partie, rien n’empêche de travailler avec un tableau dont l’élève n’utilise pas toutes les colonnes. Le tableau peut être trop grand ou bien trop petit. Dans ce cas, il est nécessaire d’agrandir le tableau à gauche ou à droite pour tenir compte de nouvelles unités de numération nécessaires à l’écriture du nombre, qu’elles fassent l’objet d’un tirage de cartes ou pas.
Comme le tableau ne comporte aucun nom d’unités de numération écrit par avance, ce sont les élèves qui doivent déterminer où placer les cartes Unité de numération. Du coup, les unités simples peuvent changer d’emplacement sur le plateau d’une partie de jeu à l’autre. Les unités simples n’ont pas vocation à toujours figurer dans la dernière colonne de droite. D’ailleurs avec les nombres décimaux, ce n’est plus le cas. Au cours d’une partie, la première unité de numération tirée est rarement celle des unités simples. Cela invite les élèves à choisir librement la position de la première unité de numération tirée. C’est au 2e tirage d’unité de numération que les élèves doivent utiliser leurs connaissances sur l’ordre des unités de numération pour déterminer son emplacement. Ils doivent éventuellement rajouter des colonnes (grâce à un plateau supplémentaire) à gauche ou à droite.
Exemple de tirages et de remplissage d’un tableau constitué d’un seul puis de deux plateaux associés :




Dans cet exemple, les élèves tirent les unités de mille au premier tirage et les posent dans la colonne du milieu. Ce choix est tout à fait correct étant donné que les joueurs ne savent pas quels seront les tirages suivant. Puis au deuxième tirage, ils tirent les dizaines. Ils doivent alors décider de prolonger leur tableau en posant une nouvelle feuille pour disposer de colonnes supplémentaires à droite. En faisant ces choix de positionnement des unités de numération, les élèves utilisent activement leurs connaissances sur l’ordre des unités de numération pour résoudre un problème. C’est tout à fait différent que de savoir réciter la comptine des unités de numération. De plus, les erreurs sont visibles pour l’enseignant qui peut alors en discuter avec eux, intervenir et rappeler le principe et son usage.
2.3. La gestion des zéros
L’utilisation de zéros est nécessaire pour pouvoir écrire le nombre hors du tableau en « calant » les autres chiffres dans la bonne unité de numération.
- Les zéros des unités de numération à droite. Des tirages de cartes peuvent conduire à l’absence de valeur pour les unités de numération à droite, que ces unités de numération correspondent à des colonnes situées sur le tableau ou bien en dehors du plateau, et qu’il ne faut pas oublier de prendre en compte pour écrire le nombre : cela permet d’apprendre le rôle des zéros à droite dans l’écriture du nombre, et donc de travailler le principe de position. Par exemple, le tirage 12 dizaines nécessite l’usage d’un zéro « à droite » pour écrire le nombre correspondant : 120.
- Les zéros des unités de numération intercalaires. Des tirages de cartes peuvent conduire à l’absence de valeurs relatives à certaines unités de numération entre des unités de numération utilisées (“des trous” dans l’écriture du nombre) : cela permet d’apprendre le rôle des zéros intercalaires dans l’écriture du nombre et donc de travailler le principe de position. Par exemple, le tirage 12 dizaines et 3 dizaines de mille nécessite l’usage d’un zéro intercalaire entre les centaines et les dizaines de milles pour écrire le nombre correspondant : 30 120.
Lors des tirages successifs d’unités de numération, les cartes ne désignent pas nécessairement des unités de numérations adjacentes, comme dans l’exemple ci-dessous avec des dizaines et des unités de mille. En particulier, il peut y avoir une absence de tirage pour les unités simples.

Dans ce cas, pour trouver le nombre mystère et l’écrire en dehors du tableau, les élèves doivent prendre en compte les unités de numération absentes. Dans l’exemple ci-dessus, il s’agit des centaines et des unités. Il faut donc inscrire un zéro dans l’écriture du nombre à l’endroit correspondant : un zéro pour le chiffre des unités et un zéro pour le chiffre des centaines.
Nous avons remarqué (Soury-Lavergne et al., 2020) que les élèves complétaient plus facilement par des zéros lorsque les unités de numération absentes étaient “à droite” que lorsqu’elles étaient intercalées entre des unités de numération. Par exemple les élèves trouvent plus facilement que 56 centaines donnent le nombre 5 600 plutôt que 56 centaines et 3 unités donnent 5 603. Cela indique que les stratégies mobilisées dans les deux cas ne sont peut être pas identiques (voir les deux principales stratégies des élèves décrites à la page « Stratégies et erreurs des élèves »).
2.4. Des nombres à 2 chiffres dans une même colonne du tableau de numération
Les tirages peuvent conduire à déposer une carte Nombre à deux chiffres (le nombre 23 dans l’exemple ci-dessus) ou bien plusieurs cartes dans une même unité de numération (il suffit que la sélection de cartes Unité de numération à disposition des joueurs contienne plusieurs fois la même unité de numération, dans l’exemple ci-dessus au moins deux fois la carte dizaines). Ces situations peuvent être déstabilisantes pour les élèves et les enseignants.
En effet, dans l’écriture d’un nombre, puisqu’il n’y a pas d’indication sur les unités numération, il n’y a qu’un seul chiffre possible par unité de numération. Cependant, cette règle implicite liée à l’écriture des nombres ne devrait pas être appliquée également de manière automatique lors de l’usage du tableau de numération (Perrin-Glorian, 2014). En effet, en permettant d’écrire des nombres à deux chiffres ou plus dans les colonnes du tableau, le nombre reste parfaitement déterminé puisque les unités de numération sont explicites et les joueurs ont à gérer ensemble le contenu de chaque unité de numération. Il est alors possible de faire apparaître la nécessité de convertir afin de n’obtenir ensuite plus qu’un nombre à un chiffre dans chaque colonne pour pouvoir écrire le nombre en dehors du tableau. Les élèves utilisent ainsi le tableau comme un outil pour faire les conversions et pas seulement pour contrôler la position relative des cartes. On amène ainsi les élèves à travailler précisément le principe décimal et à comprendre le lien entre écriture chiffrée du nombre et valeur représentée.
Lorsqu’il y a des nombres à 2 chiffres dans une même colonne, cela nécessite la conversion vers l’unité de numération immédiatement supérieure et donc le travail du principe décimal
Lorsque plusieurs nombres sont posés dans une même colonne, le traitement par addition des nombres permet d’obtenir la valeur totale pour cette unité de numération et conduit, si nécessaire, à la conversion vers l’unité de numération immédiatement supérieure (conversion vers la gauche) et donc le travail du principe décimal..

Dans le tirage ci-contre, pour passer de 23 unités de mille, 5 dizaines de mille et 7 dizaines au nombre 73 070, il faut faire des
calculs locaux et plusieurs conversions. Tout d’abord au niveau des dizaines, il faut considérer que 4 dizaines et 3 dizaines font 7 dizaines : 4 d + 3 d = 7 d
Pour les unités de mille, il faut décomposer 23um en 20um et 3um puis convertir les 20um en 2 dizaines de mille.
23 um = 20 um + 3 um et 20 um = 2 dm donc 21 um = 2 dm + 3 um
Enfin, comme il y a déjà 5 dizaines de mille, avec les 2 dizaines de mille issues de la conversion, il y a en tout 7 dizaines de mille.
Le nombre s’écrit donc 73 070 hors du tableau. La position de chaque chiffre désigne sans ambiguïté une seule unité de numération. Dans l’écriture 73 070 résultant des conversions, les élèves peuvent plus facilement repérer le fait qu’il y a 3 unité de mille mais aussi 23 unités de mille si nécessaire, ou encore 73 unités de mille etc…
Toute une variété de configurations apparaissent au cours des parties. Par exemple :

Plusieurs cartes de nombres à 1 chiffre dans une même colonne, mais le résultat s’obtient sans conversion.

Plusieurs cartes de nombres à 1 chiffre dans une même colonne, avec une conversion nécessaire de 10 unités en une dizaine pour obtenir le résultat. En effet, dans la colonne des unités, il y a 12 unités.

Plusieurs cartes de nombres à 2 chiffres sont dans une même colonne et le résultat s’obtient après plusieurs conversions. Des colonnes non étiquetées (dizaines et dizaines de mille) sont à prendre en compte pour écrire le nombre. Les chiffres correspondant à ces unités de numération résultent d’une conversion. Par exemple, il faut convertir 23 unités de mille en 20 unités de mille + 3 unité de mille, c’est-à-dire 2 dizaines de mille et 3 unité de mille.
3. Approfondissements didactiques sur la numération
La numération décimale de position est la façon usuelle d’écrire les nombres avec les chiffres. Il y a exactement 10 chiffres distincts (0, 1, 2, 3, 4 5, 6, 7, 8 et 9) pour écrire l’infinité des nombres entiers naturels et les nombres décimaux. La combinaison de ces chiffres pour désigner sans ambiguïté chacun des nombres suit deux principes :
- le principe de position : chaque chiffre désigne une unité de numération selon sa position dans le nombre ;
- le principe décimal : chaque nombre peut être décomposé en unités, dizaines, centaines ou toute autre unité de numération.
Maîtriser la numération décimale de position, c’est maîtriser ces deux principes (d’ailleurs la dénomination indique en elle même ces deux principes).
Le jeu du Chiffroscope contribue à cet apprentissage en amenant les élèves à utiliser les différentes unités de numération selon différents points de vue, comme l’illustre l’exemple de la centaine qui peut être considérée respectivement comme :
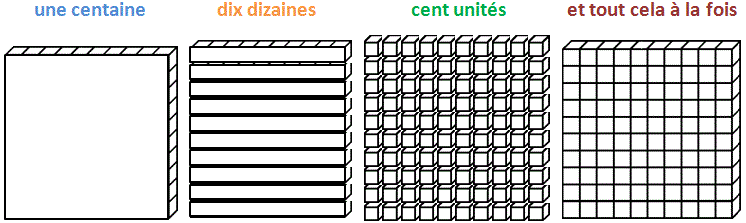
3.1 Comment caractériser ce que savent les élèves en numération décimale de position ?
Les didacticiens utilisent la notion de conception pour décrire les connaissances des élèves (Vergnaud 1990 ; Balacheff & Margolinas, 2005). Il s’agit de décrire et mieux comprendre la façon de savoir des élèves, y compris quand ils ne produisent pas les réponses attendues. Même lorsqu’ils se trompent, les élèves utilisent leur connaissances. Pour enseigner, il est alors très utile de comprendre ce que font et « comment savent » les élèves pour ensuite leur proposer les situations et les aides adéquates.
Au cours de nos expérimentations du Chiffroscope, dans sa version numérique avec un robot (projet OCINAEE puis LéA CiMéLyon (Croquelois et al., 2019) ) ou sa version papier telle que présentée sur ce site, nous avons eu de multiples occasions d’observer les procédures et stratégies des élèves. En effet, le fait de les voir manipuler les cartes, de discuter en binôme et d’écrire leurs calculs, nous a permis d’accéder à une partie de leur raisonnement en numération. Nous avons pu repérer certaines régularités dans leurs actions et leurs décisions. Ces régularités dans l’action sont constitutives de la connaissance, de la façon dont les élèves conceptualisent l’écriture des nombres pour ce qui concerne le Chiffroscope : « Au fond de l’action, la conceptualisation » nous dit Gérard Vergnaud (2011, p. 275).
Nous avons donc cherché à identifier des « invariants opératoires » c’est à dire des régularités dans l’action de l’élève pour résoudre les problèmes posés par le Chiffroscope. Nous considérons que ces régularités sont caractéristiques des différentes conceptions. Nous avons réussi à distinguer six invariants opératoires relatifs à la numération dans les stratégies des élèves. Il y en a surement d’autres à identifier. Nous avons rattachés trois de ces invariants opératoires au principe de position (c’est-à-dire qu’un de ces invariant opératoire décrit une façon qu’à l’élève de connaitre le principe de position) et les trois autres au principe décimal. L’identification et la définition de ces invariants opératoires s’est faite progressivement en les confrontant à l’observation des stratégies des élèves en résolution de problème dans le cadre des travaux du LéA CiMéLyon (Soury-Lavergne, 2020).
Six invariants opératoires pour modéliser les conceptions des élèves relatives à la numération décimale de position
Trois invariants opératoires relèvent du principe de position :
Ordre des unités de numération : Cet invariant opératoire se manifeste lorsque l’élève positionne les unités de numération dans l’ordre conventionnel, c’est-à-dire de droite à gauche pour les unités d’ordre de plus en plus grand. Concrètement, l’élève est capable de positionner les cartes Unité de numération dans le bon ordre ou est capable de dire que « les dizaines c’est à gauche des unités ».
Gestion des zéros à droite ou gestion des zéros intercalaires : Il s’agit de deux invariants opératoires distincts qui se manifestent lorsque les zéros sont utilisés pour positionner les autres chiffres du nombre au bon endroit, c’est-à-dire en regard de la bonne unité de numération.
L’invariant opératoire zéros à droite permet de compléter par des zéros l’écriture d’un nombre de façon à positionner le chiffre non nul le plus à droite en relation avec la bonne unité de numération (c’est-à-dire placer respectivement un zéro aux unités, ou deux zéros pour les dizaines et les unités pour qu’un chiffre non nul soit bien respectivement un chiffre de dizaines ou de centaines). Concrètement, l’élève est capable de considérer que s’il a 2 dizaines, il faut que le chiffre 2 soit au rang des dizaines et donc qu’il faut un 0 au rang des unités.
L’invariant opératoire zéros intercalaires permet de décrire l’action de placer des zéros entre deux chiffres non nuls, pour les positionner les chiffres non nuls avec leur unité de numération. Concrètement, l’élève est capable de considérer que s’il a un nombre constitué de 3 centaines et 5 unités, pour que le chiffre 3 soit au rang des centaines et le chiffre 5 au rang des unités, il faut placer un 0 au rang des dizaines.
Ces deux invariants ont dû être distingués car la gestion correcte des zéros à droite est apparue dans les productions des élèves beaucoup plus souvent que le second (une partie de l’explication résidant dans le fait qu’il produit la même réponse que l’invariant opératoire retour à l’unité).
Trois invariants opératoires relèvent du principe décimal :
Retour à l’unité : Cet invariant opératoire rend compte de la conversion des unités de numération en unités simples (1 centaine = 100 unités ou 1 millier = 1000 unités). Concrètement, l’élève est capable de convertir un nombre donné dans une unité en unités simples : 12 dizaines = 120 (implicitement 120 unités)
Conversion entre unités : Cet invariant opératoire rend compte de la conversion des unités de numération entre elles, qu’elles soient adjacentes ou non, mais sans passage à l’unité simple (Exemple : 1 millier = 100 dizaines sans qu’il s’agisse du résumé de la procédure qui consiste à convertir 1 millier en 1000 unités puis à utiliser la conversion 10 unités = 1 dizaine pour obtenir 1000/10 = 100 dizaines). Concrètement, l’élève est capable de convertir un nombre donné dans une unité en une autre unité : 120 dizaines = 12 centaines ou 12 dizaines = 1,2 centaines ou 1,2 unités = 12 dixièmes…. Le plus simple est quand les unités sont adjacentes, mais cela est aussi possible entre unités non adjacentes : 1200 unités = 12 centaines, 12 unités = 1200 centièmes…
Conversion avec retenue : Cet invariant opératoire rend compte du fait que lorsqu’il est nécessaire d’additionner au sein d’une unité de numération et que le résultat fait apparaître un nombre supérieur à 9, alors la conversion vers l’unité de numération supérieure est réalisée. Par exemple, avec le tirage 8 dizaines puis 4 dizaines puis 3 centaines : l’élève considère qu’il obtient 12 dizaines (8+4=12), donc par conversion 1 centaine et 2 dizaines, la centaine obtenue devient une retenue sur les 3 centaines déjà présentes. Le résultat est alors 4 centaines et 2 dizaines, soit 420.
Un grand nombre de réponses incorrectes différentes : d’autres invariants opératoires à identifier
Il est très intéressant de noter la grande variété des réponses incorrectes fournies par les élèves. Pour certains exercices résolus par plusieurs centaines d’élèves, nous avons récolté une soixantaine de réponses et même parfois jusqu’à 160 réponses incorrectes différentes !
Au cours de ce travail nous avons fait des hypothèses sur les invariants opératoires autres que les 6 présentés précédemment. Même si un grand nombre de réponses incorrectes restent encore inexplicables, un certain nombre peuvent s’expliquer par la mise en oeuvre de l’un ou l’autre des invariants opératoires présentés ci-dessous, voire une combinaison de plusieurs d’entre-eux.
Unité de numération décalée à droite : « Le chiffre le plus à gauche dans le nombre devient l’unité de l’unité de numération considérée (sauf pour les unités) ». Par exemple, avec 12 dizaines, l’élève considère que c’est 1 qui est le chiffre des dizaines autrement dit que 12 dizaines = 1 dizaine et 2 unités. Cet invariant opératoire est efficace et produit une réponse correcte lorsque chaque unité de numération ne contient que des nombres à un chiffre. Mais il produit une réponse erronée dès qu’une unité de numération contient un nombre à deux chiffres.
Somme des nombres : Cet invariant opératoire se manifeste lorsque les nombres obtenus pas les tirages des cartes Nombre sont simplement ajoutés sans prendre en compte les unités de numération associées. Chaque nombre est considéré comme des unités. Par exemple, le tirage 15 centaines, 8 dizaines et 6 unités donne le nombre 29 (car 29 = 15+8+6) au lieu de 1 586.
Ordre inversé : Cet invariant opératoire se manifeste lorsque les unités de numération sont positionnées dans l’ordre inverse de l’ordre conventionnel. Les élèves confondent l’ordre des unités de numération pour l’écriture du nombre avec la position des nombres sur la droite numérique. En comparaison avec le nombre 5, un nombre constitué de 5 centaines aura le chiffre 5 plus à gauche dans son écriture, mais sera positionné plus à droite sur la droite numérique.
Juxtaposition des unités de numération : Cet invariant opératoire se manifeste lorsque les nombres associés à des unités de numération sont juxtaposés sans conversion pour obtenir l’écriture du nombre. Par exemple, le tirage 52 centaines, 8 milliers, 31 dizaines et 9 unités devient 852 319.
Concaténation : Cet invariant opératoire se manifeste lorsque les nombres du tirage sont utilisés pour écrire le nombre, sans prise en compte de l’unité de numération respective. Il sont simplement écrits les uns à côtés des autres. Exemple : le tirage 12 unités, 20 milliers et 7 dizaines devient le nombre 12 207.
3.2. Les principales conceptions des élèves sur la numération décimale de position
Notre analyse didactique des connaissances des élèves en numération décimale de position, repose sur l’identification de que savent les élèves quand bien même leurs réponses ne sont pas correctes. Nous avons pu le faire en repérant trois invariants opératoires qui permettent de caractériser la façon dont les élèves savent gérer l’ordre des unités de numération et les zéros (à droite ou intercalés) et trois invariants opératoires qui caractérisent les connaissances des élèves sur les conversions (retour à l’unité, conversion entre unités et conversion avec retenue). Lorsqu’un élèves utilise un seul de ces invariants opératoires, il manifeste une certaine connaissance de la numération, bien qu’encore insuffisante pour réussir tous les problèmes posés par le Chiffroscope.
Notre hypothèse est que les conceptions permettant d’expliquer la plupart des réponses des élèves dans les problèmes de numération sont principalement :
- Une conception « position » qui inclut uniquement les invariants opératoires rattachés au principe de position (ordre, zéros à droite et zéros intercalaires). Cette conception décrit la façon de savoir d’un élève qui répond correctement à un problème tel que dire quel est le chiffre des dizaines dans 123, ou bien écrire correctement le nombre qui correspond à 1 unité et 5 dixièmes : 1,5, ou encore 2 unités + 4 centaines = 402. En revanche, il va échouer à trouver le nombre correspondant à 24 dizaines et 3 centaines.
- Une conception « retour à l’unité » qui utilise essentiellement l’invariant opératoire « retour à l’unité ». Cette conception décrit la façon de savoir d’un élève qui considère les nombres uniquement en unités simples. 12 dizaines n’est pas un nombre, mais il sait le transformer en un nombre en convertissant en unités : 12 dizaines = 120 (unités simples est implicite). Cet élève réussit de nombreuses taches, mais sera bloqué au moment de travailler sur les grandeurs et d’exprimer les mesures d’une grandeur en utilisant différents nombres ( pour cet élève, 12 milliers ou 12k ne peut pas exprimer la même valeur que 12 000). Il sera aussi en difficulté avec les nombres décimaux, car l’unité simple ne sera plus utilisable comme référence commune pour les conversions.
- Une conception « décimale » qui inclut quatre invariants opératoires, les trois relatifs à la position et l’invariant conversion entre unités (qui permet aussi la conversion à l’unité simple). C’est la conception de référence, vers laquelle tend l’enseignement avec le Chiffroscope.
4. Références bibliographiques
Balacheff, N., & Margolinas, C. (2005). CKȼ Modèle de connaissances pour le calcul de situations didactiques. In C. Margolinas & A. Mercier (Éds.), École d’Été de Didactique des Mathématiques (hal- 01139408) p. 1‑32. La pensée Sauvage Grenoble, France.
Croquelois, S., Martinez, J.-L., Rabatel, J.-P., & Soury-Lavergne, S. (2019). Du projet collaboratif à la formation : Continuité des apprentissages et de l’enseignement de la numération du cycle 2 au cycle 3. Actes du 46e colloque de la COPIRELEM. 643-652. Lien
Mounier, E. (2012). Des modèles pour les numérations orales indo-européennes à usage didactique, application a la numération parlée en France,. Annales de Didactique et de Sciences Cognitives, 17, 27‑58.
Perrin-Glorian, M.-J. (2014) Contribution aux travaux des groupes d’élaboration des projets de programmes C2, C3 et C4, Conseil National des Programmes. Lien
Soury-Lavergne, S., Croquelois, S., Martinez, J.-L., & Rabatel, J.-P. (2020). Conceptions des élèves de primaire sur la numération décimale de position. Revue Maths Ecole, 233, 128‑143. Lien
Vergnaud, G. (1990). La théorie des champs conceptuels. Recherches en Didactique des Mathématiques, 10(2.3), 133‑170.
Vergnaud, G. (2011). Au fond de l’action, la conceptualisation. In Savoirs théoriques et savoirs d’action (p. 275‑292). Presses Universitaires de France; Cairn.info. https://doi.org/10.3917/puf.barbi.2011.01.0275
