3.4. Critères pour sélectionner les cartes des parties de jeu
Pour que les parties de jeu soient productives pour les élèves en termes de stratégie et d’apprentissage, il faut que les tirages produisent des configurations intéressantes. Cela est partiellement contrôlable en sélectionnant le lot de cartes avec lesquelles jouent les élèves. Il est possible de sélectionner des cartes nombres et des cartes unités de numération d’une certaine façon pour que les parties amènent les élèves à travailler le principe de position, à s’interroger sur la place des zéros et à faire des conversions entre unités de numération.
Il faut également que les sélections correspondent au niveau scolaire de vos élèves. Or, les sélections de cartes ne sont pas repérées et différenciées par niveau scolaire (FAQ), mais uniquement par domaine numérique. C’est un choix pédagogique qui permet à chaque élève de travailler dans un domaine numérique adapté à ses compétences et non a priori dicté par le niveau scolaire de sa classe. Cela permet à chaque élève d’évoluer à son rythme sans ressentir de décalage par rapport à des attendus de niveau scolaire parfois inadaptés (trop simples ou trop difficiles).
Ci-dessous, voici les sélections de cartes possibles et les explications sur comment réaliser des sélections de cartes et déterminer un nombre de cartes pour obtenir des parties de jeu intéressantes pour travailler différents aspects de la numération décimale de position. Avec ces informations, vous pouvez vous aussi concevoir vous même de nouvelles séries de cartes-nombres et de cartes-unités de numération pour les adapter à vos objectifs spécifiques et aux besoins de vos élèves.
3.4.1. Sélections de cartes Unité de numération pour choisir le domaine numérique de travail
C’est avec la sélection de cartes unités de numération que le domaine numérique est déterminé (et non la référence à un niveau de classe).
En plus du domaine numérique, le choix des unités de numération avec lesquelles travaillent les élèves permet de privilégier le principe de position ou le principe décimal. S’il y a une carte pour chaque unité de numération, il y aura peu de conversions et plutôt un travail sur le principe de position avec la gestion des zéros. S’il y a plusieurs cartes pour la même unité de numération, l’aléatoire du jeu conduit à ce qu’il y ait davantage de conversions, et donc favorise le travail du principe décimal. Cependant, l’aléatoire du jeu ne garantit pas que chaque partie amène les élèves à travailler systématiquement chaque principe.
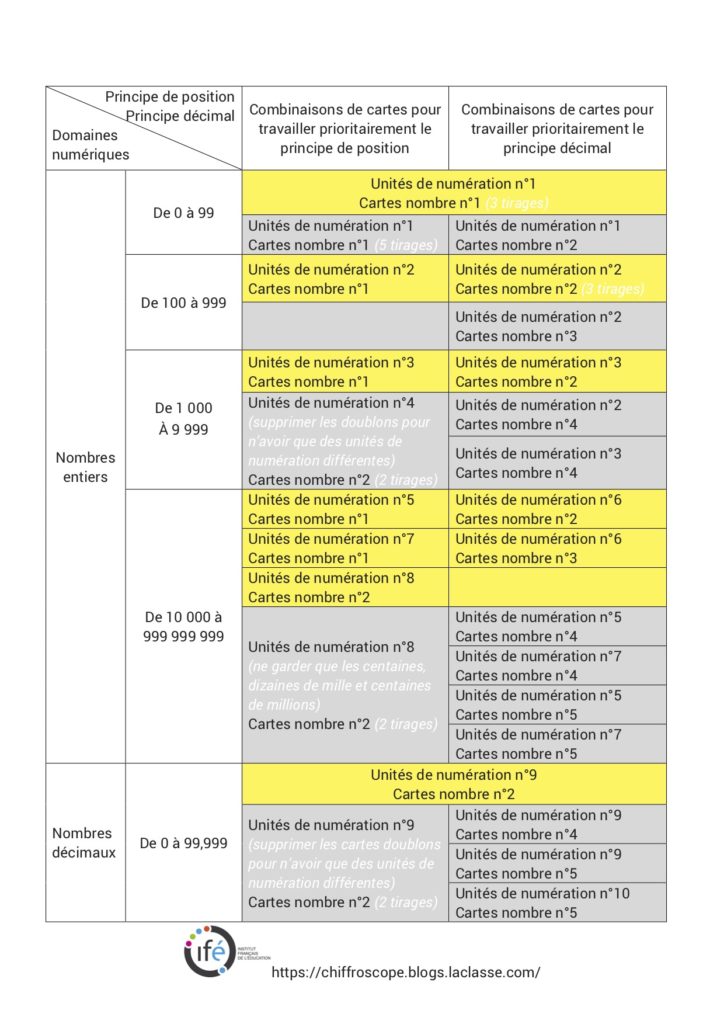
- Les nombres entiers de 0 à 99 : faire travailler les élèves avec seulement les unités et les dizaines (sélection U1)
- Les nombres entiers de 100 à 999 : faire travailler les élèves avec unités, dizaines, centaines (sélection U2)
- Les nombres entiers de 100 à 9 999 : faire travailler les élèves avec (sélection U3 et U4)
- Les nombres entiers de 10 000 à 999 999 999 : faire travailler les élèves avec (sélection U5, U6, U7 et U8)
- Les nombres décimaux de 0 à 99,999 : faire travailler les élèves avec (sélection U9 et U10)
Cartes Unité de numération Sélection 1 – U1 – Nombre mystère < 99

Cette sélection ne contient que les unités et les dizaines, deux unités de numération différentes et adjacentes. Cette sélection est à privilégier pour l’étude des nombres inférieurs à 100 avec la sélection de cartes-nombres n°1. Associées à la sélection de cartes-nombre n°2 (voir), le tirage peut parfois conduire à un nombre cible à 3 chiffres.
Cartes Unités de numération Sélection 2 – U2 – Nombre cible < 999

Cette sélection propose trois unités de numération différentes et adjacentes. Elle permet d’écrire des nombres jusqu’aux milliers selon le tirage des cartes-nombres.
Pour éviter des nombres cibles à 4 chiffres (aux milliers) tout en travaillant avec les cartes nombres de 0 à 99, il faut retirer les cartes centaines de la sélection.
Cartes Unités de numération Sélection 3 – U3 – Nombre cible < 9 999

Cette sélection propose quatre unités de numération différentes et adjacentes. Elle permet d’écrire des nombres jusqu’aux dizaines de mille selon le tirage des cartes-nombres. Avec un tirage réduit à trois cartes, on favorise l’apparition de colonnes vides intercalées et donc la gestion des conversions ou des zéros.
Cartes Unités de numération Sélection 4 – U4 – Nombre cible < 9 999

Cette sélection propose trois unités de numération différentes et non adjacentes. Elle permet d’écrire des nombres jusqu’aux dizaines de mille selon le tirage des cartes-nombres. Quel que soit le tirage, il va conduire à écrire un nombre cible comportant un zéro au moins aux unités. Les centaines sont absentes du tirage. Selon le tirage, le chiffre des centaines du nombre cible sera un zéro ou bien résulte de la conversion des dizaines.
Cette sélection permet d’aborder les points clefs, gestion des zéros et conversions, avec des nombres relativement petits. Elle est adaptée pour le cycle 2 et le cycle 3.
Cartes Unités de numération Sélection 5 – U5 – Nombre cible < 9 999 999

Cette sélection propose quatre unités de numération différentes, dont trois non adjacentes. Quel que soit le tirage, elle va conduire à écrire un nombre comportant un zéro au moins aux unités. Elle permet d’écrire des nombres cibles jusqu’aux dizaines de millions selon le tirage des cartes-nombres.
Les unités de numération nécessaires à l’écriture du nombre mais absentes du tirage (centaines et centaines de mille, peut être dizaines de millions), peuvent néanmoins avoir un chiffre différent de zéro, résultant d’une conversion de l’unité adjacente. On peut favoriser le travail des zéros ou bien le travail des conversion, en choisissant de faire tirer peu de cartes ou bien jusqu’à 5 cartes nombres. De façon générale, pour les nombres cibles assez grands, le nombre de cartes dans le tirage influence le type de stratégie à mettre en œuvre (trois tirages pour travailler les zéros, quatre ou cinq de tirages pour travailler les conversions).
Cartes Unités de numération Sélection 6 – U6 – Nombre cible < 9 999 999

Cette sélection propose quatre unités de numération différentes et adjacentes.
Cette sélection, quel que soit le tirage, va conduire à écrire un nombre comportant un zéro au moins aux unités, dizaines, centaines et unités de mille.
Elle permet d’écrire des nombres jusqu’aux dizaines de millions selon le tirage des cartes-nombres.
Les unités adjacentes contigües devraient favoriser les conversions, faciles ou difficiles selon le choix des cartes-nombres.
Cartes Unités de numération Sélection 7 – U7 – Nombre cible < 999 999 999

Cette sélection propose cinq unités de numération différentes dont trois adjacentes.
Cette sélection, quel que soit le tirage, va conduire à écrire un nombre comportant un zéro au moins aux unités et aux dizaines.
Elle permet d’écrire des nombres jusqu’aux unités de milliards selon le tirage des cartes-nombres.
Les unités de numération nécessaires à l’écriture du nombre mais absentes du tirage (unités de mille et dizaines de millions, unités de milliards peut être), peuvent avoir un chiffre différent de zéro selon le tirage des cartes nombres dans les colonnes adjacentes et les conversions correspondantes.
Cartes Unités de numération Sélection 8 – U8 – Nombre cible < 999 999 999

Cette sélection propose les neuf unités de numération différentes et adjacentes nécessaires à l’écriture des nombres jusqu’aux centaines de millions, et selon le tirage des cartes-nombres, jusqu’aux unités de milliards.
L’enseignant peut choisir de proposer aux élèves l’ensemble des cartes. Dans ce cas, il est probable que des unités intercalaires ne feront pas l’objet d’un tirage et conduiront à un zéro ou une conversion. Il peut aussi choisir ou seulement une sélection d’unités, adjacentes favorisant les conversions entre unités adjacentes avec un certain nombre de zéros intercalaires ou en fin de nombre. Il peut aussi choisir une sélection d’unités non adjacentes ou pas, favorisant alors la gestion des zéros, mais il est probable que d’éventuelles conversions passent totalement inaperçues et viennent compléter des colonnes vides sans que l’élève en ait conscience.
Cartes Unités de numération Sélection 9 – U9 – Nombres décimaux

Cette sélection propose quatre unités de numération différentes et adjacentes
Cette sélection permet d’écrire des nombres jusqu’aux centièmes et aux centaines selon le tirage des cartes-nombres.
Cette configuration permet d’explorer les nombres décimaux. Le retour à l’unité, stratégie couramment pratiquée avec les nombres entiers, ne pourra plus être mobilisée telle quelle. Les élèves vont devoir trouver d’autres stratégies pour résoudre le problème posé et se référer à d’autres unités de numération.
Cartes Unités de numération Sélection 10 – U10 – Nombres décimaux

Cette sélection propose trois unités de numération différentes et non adjacentes.
Les unités simples et les centièmes ne font pas l’objet d’un tirage. Les unités simples seront gérées par un zéro ou par la conversion provenant des dixièmes. Les centièmes par un zéro ou la conversion avec les millièmes.
Selon les cartes-nombres choisies, cette sélection porte sur le traitement de la conversion entre les dixièmes et les unités simples. Très souvent, les élèves séparent la partie entière de la partie décimale et ont beaucoup de difficulté à considérer ces deux parties comme constituants d’un même nombre et traiter ensemble les deux parties du nombre, notamment avec les conversions entre les dixièmes et les unités simples.
Cette sélection peut contraindre à des conversions avec des unités de numération absentes du tirage, dont les unités, et la place de la virgule se posera pour écrire le nombre hors du tableau.
Lien vers récapitulatif et téléchargement
3.4.2. Les critères pour constituer des sélections de cartes nombre, exemple de sélection
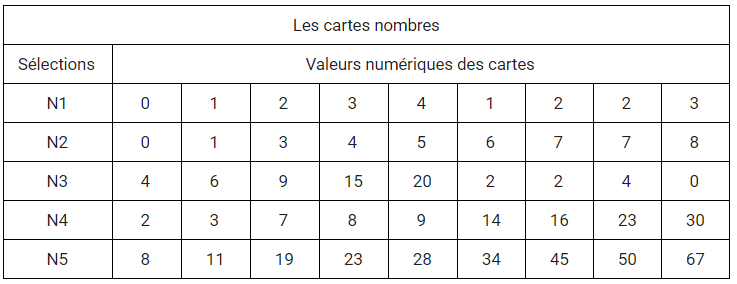
Nous proposons cinq sélections de cartes nombres ne contenant que des nombres à 1 chiffre ou mélangeant des nombres à 1 ou 2 chiffres. Nous expliquons les conséquences sur les types de tirages et les stratégies privilégiées pour les élèves.
Photos des sélections : cases séparées comme des cartes juxtaposées mais non collées
Cartes Nombres Sélection n°1

Cette sélection de nombres évite a priori les conversions entre unités de numération. C’est la sélection la plus simple possible, qui n’aborde que peu d’éléments intéressants dans le jeu. Elle est utile pour les CP, au tout début.
Cartes Nombres Sélection n°2

Avec plusieurs cartes plus grandes que 5, le total des cartes nombres tirées dans une même unité de numération peut être supérieur à 9. Le tirage conduit alors à devoir effectuer une conversion entre deux unités de numération.
Le fait d’aborder les conversions avec les élèves est un point important du jeu. Néanmoins, si, dans un 1er temps, vous souhaitez éviter cette configuration tout en travaillant avec les nombres cibles de 0 à 99, il faut retirer les quatre cartes 6-7-7-8 de la sélection et faire jouer les élèves avec un tirage de 3 cartes associées aux unités de numération unités et dizaines.
Cartes Nombres Sélection n°3

Cette sélection introduit des nombres à deux chiffres. Elle offre la possibilité d’un tirage nécessitant des conversions, mais avec une probabilité réduite qui ne devrait pas apparaître à chaque partie. De même les conversions en cascades sont réduites.
Elle n’est pas très pertinente pour travailler les grands nombres, sauf pour apprendre à gérer les zéros (et le principe de position).
Cartes Nombres Sélection n°4

Cette sélection de cartes nombres propose des nombres à un chiffre proches de 10 et des nombres à deux chiffres qui entraineront le passage à la dizaine supérieure dans l’addition au sein d’une unité de numération et la nécessité de conversions.
Cartes Nombres Sélection n°5

L’intérêt de cette sélection est qu’elle permet de travailler des grands nombres cibles tout en nécessitant une stratégie de conversion. Elle peut cependant conduire à des conversions en cascade, notamment si le nombre cible n’est pas très grand. Elle ne doit être proposée aux élèves qu’une fois qu’ils ont pu travailler et discuter des conversions. Cette sélection de cartes nombres est plus intéressante à utiliser pour travailler les nombres à plus de 5 chiffres, afin qu’il y ait besoin de faire des conversions et d’utiliser des zéros. Avec des nombres cibles à 3 ou 4 chiffres, le travail devient plus technique, calculatoire. Cela peut intéresser des élèves qui ont besoin d’aller plus loin et de développer leur expertise.
Par exemple : avec un tirage de 45d et 67d = 112d
112d = 110d + 2d
110d = 100d + 10d
10d = 1c
100d = 10c = 1um
→ 112d = 1um et 1c et 2d → le nombre s’écrit 1 120
Résumé des sélections de cartes Nombre proposées
3.4.3. Combiner les sélections de cartes unités de numération et cartes nombres
Sélections de cartes pour travailler prioritairement le principe de position
- Choisir des cartes-nombres avec uniquement des nombres à 1 chiffre inférieurs à 5 (par exemple la sélection N1 ou une partie de N2 §…)
- Choisir peu d’unités de numération différentes (3 ou 4 maximum) qu’elles soient contiguës ou pas
- Pendant la partie de jeu, restreindre le nombre à 2 ou 3 tirages (un tirage = une carte nombre associée à une carte unité de numération)
- Si utilisation de toutes les cartes nombres des sélections N1 ou N2, présence de 6, 7 et 8, alors des conversions relativement faciles peuvent apparaître
- Enlever des unités de numération pour faire apparaître des trous c’est-à-dire des unités de numération non contigües et avoir autant de cartes-nombres à 1 chiffre que d’unités de numération différentes.
Sélection de cartes pour travailler prioritairement le principe décimal
- Choisir des cartes-nombres à 1 chiffre (sélection N1 ou N2)
- Utiliser des unités de numération contiguës
- Pendant la partie, prévoir entre 3 et 5 tirages
- Avec toutes les cartes N1, des conversions relativement faciles peuvent apparaître
- Choisir les sélections de cartes-nombre N2 ou N3 et des cartes unité de numération non contigües (U?): les conversions prendront le pas sur la position
- Avec les sélections de cartes-nombre N2, N3, N4 et N5, les conversions prendront le pas sur la position surtout dans le cas d’une partie de jeu à 5 tirages (un tirage = une carte nombre associée à une carte unité de numération)
Partie facile, partie difficile, niveau de classe
Les parties sont a priori plus faciles avec des cartes-nombres à 1 chiffre et plus difficiles avec des cartes-nombres à 2 chiffres. Mais c’est un peu plus complexe, car cela dépend du nombre de tirages et de la sélection des unités des numération. La difficulté d’une partie résulte plutôt des éléments suivants, bien que la dimension aléatoire du jeu ne permette pas de certifier le niveau de difficulté d’une partie :
- des nombres sur les cartes nombres : les nombres à 1 chiffre pour les parties faciles, les nombres à 2 chiffres pour les parties difficiles
- des unités de numération : des unités de numération non adjacentes pour des parties faciles et peu d’unités de numération différentes et adjacentes pour des parties plus difficiles
- du nombre de tirages : peu de tirage (3) pour les parties faciles, 4 ou 5 tirages pour les parties plus difficiles.
Puisque l’aléatoire du jeu ne permet pas de contrôler complètement le niveau de difficulté des parties, les Arrêts sur image sont le moyen de proposer aux élèves des parties bien adaptées.
Par ailleurs, les niveaux de classe ne sont pas indiqués. Seuls les domaines numériques travaillés sont précisés et vous permettent de proposer à vos élèves des situations et des contextes numériques adaptés à leurs besoins, sans stigmatisation liée à un niveau de classe différent du leur.
3.4.4 Le tableau de jeu
Le plateau de jeu est constitué par ce tableau de numération aux colonnes sans nom prédéfini de format A4 en portrait. Les dimensions des feuilles autorisent leur placement sur une table classique d’élèves telle qu’on les rencontre assez fréquemment. Cette feuille comporte/ ce tableau se compose de 3 colonnes complètes et 2 demi-colonnes de chaque côté. La largeur des colonnes correspond aux dimensions des cartes-nombres et des cartes-unités de numération. Les demi-colonnes de deux feuilles peuvent être assemblées bord à bord et constituer une colonne entière pour agrandir le tableau vers les unités manquantes sur la 1ère feuille, aussi bien à gauche qu’à droite.
Il est nécessaire de laisser à la disposition des élèves un nombre suffisant d’exemplaires de ce tableau 3 + 2 ½colonnes. En effet, il est important qu’ils puissent décider eux-mêmes de l’agrandir à gauche comme à droite, autant que nécessaire, selon leurs besoins d’unités de numération.
