3.5. Approfondissements didactiques sur la numération

Maîtriser la numération décimale de position, c’est maîtriser les deux principes sur lesquels repose la numération décimale de position :

le principe de position (chaque chiffre désigne une unité de numération selon sa position dans le nombre)
le principe décimal (chaque nombre peut être décomposé en unités, dizaines, centaines ou toute autre unité de numération).

Ce jeu amène les élèves à utiliser les différentes unités de numération selon différents points de vue, comme l’illustre l’exemple de la centaine qui peut être considérée respectivement comme :

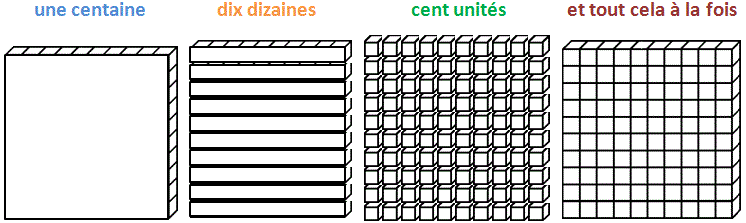
(extrait du site http://numerationdecimale.free.fr/)

Liens vers les actes C21 2019 et 2018 et RMé

3.5.1. Comment caractériser ce que savent les élèves en numération décimale de position ?

Les conceptions des élèves comme moyen de décrire leurs connaissances en numération décimale de position

« Au fond de l’action, la conceptualisation » (Vergnaud, 2011, p. 275)

Nous avons modélisé les connaissances en terme de conceptions, au sens de Balacheff dans (Balacheff & Margolinas, 2005) pour pouvoir traiter de la même façon toutes les productions des élèves, qu’elles soient correctes ou pas, en considérant qu’elles sont la manifestation d’une connaissance dans la tradition de l’épistémologue Bachelard (1934). S’appuyant sur les travaux de Vergnaud (1990), Balacheff propose de décrire une conception à partir d’un quadruplet d’ensembles (problèmes, systèmes de représentation, opérateurs, structures de contrôle). Nous n’avons eu besoin que d’une partie du modèle pour obtenir des descriptions de conceptions relatives à la numération décimale, suffisamment cohérentes et opérationnelles pour notre projet. Nous avons débuté en établissant la liste des problèmes, systèmes de représentations et opérateurs qui apparaissent dans ces conceptions :

les problèmes que la conception permet de résoudre : problèmes de codage, c’est à dire produire une désignation pour chaque nombre (infinité de nombres et quantité réduite de symboles), problème de dénombrement de collections, problème de constitution de collections d’un cardinal donné, problème de conversion, comparaison et de calcul à partir d’un répertoire restreint de résultats connus pour les premiers nombres
les systèmes de symboles qui sont mobilisés dans la résolution des problèmes : les chiffres, les positions de gauche à droite, les mots des unités de numération « unités », « dizaines », « centaines », « dixièmes », la virgule, les tableaux et les organisations spatiales des algorithmes de calculs
les opérateurs ou invariants opératoires (chez Vergnaud) qui résolvent les problèmes : association position-unité de numération, conversions, retenue, groupement, échange, comparaison à partir de l’écriture…

Nous avons cherché à identifier les invariants opératoires caractéristiques des différentes conceptions en partant du principe de position et du principe décimal. Les deux principes de la numération se sont avérés insuffisants pour caractériser et différencier les conceptions des élèves et expliquer les réponses qu’ils produisent. En particulier, ils n’ont pas permis à eux seuls de décrire les stratégies de résolution observables et de les rattacher à différentes conceptions. Nous avons alors distingué six invariants opératoires relatifs à la numération dans les stratégies des élèves que nous avons rattachés, pour trois d’entre eux, au principe de position et pour les trois autres au principe décimal (Figure 1). L’identification et la définition de ces invariants opératoires s’est faite progressivement en les confrontant à l’observation des stratégies des élèves en résolution de problème dans le cadre des travaux du LéA CiMéLyon (Croquelois et al., 2019).

Six invariants opératoires pour modéliser les conceptions relatives à la numération décimale de position

Trois invariants opératoires relevant du principe de position

Ordre des unités de numération : Cet invariant opératoire se manifeste lorsque l’élève positionne les unités de numération dans l’ordre conventionnel, c’est-à-dire de droite à gauche pour les unités d’ordre de plus en plus grand.

Gestion des zéros à droite ou gestion des zéros intercalaires : Il s’agit de deux invariants opératoires distincts qui se manifestent lorsque les zéros sont utilisés pour positionner les autres chiffres du nombre au bon endroit, c’est-à-dire en regard de la bonne unité de numération. L’invariant opératoire zéros à droite permet de compléter par des zéros un nombre de façon à positionner le chiffre non nul le plus à droite en relation avec la bonne unité de numération (c’est-à-dire placer respectivement un zéro aux unités, ou deux zéros pour les dizaines et les unités pour qu’un chiffre non nul soit bien respectivement un chiffre de dizaines ou de centaines). L’invariant opératoire zéros intercalaires permet de décrire l’action de placer des zéros entre deux chiffres non nuls, pour les positionner les chiffres non nuls avec leur unité de numération. Ces deux invariants ont dû être distingués car la gestion correcte des zéros à droite est apparue dans les productions des élèves beaucoup plus souvent que le second (une partie de l’explication résidant dans le fait qu’il produit la même réponse que l’invariant opératoire retour à l’unité).

Les invariants opératoires relevant du principe décimal

Retour à l’unité : Cet invariant opératoire rend compte de la conversion des unités de numération en unités simples (1 centaine = 100 unités ou 1 millier = 1000 unités).

Conversion entre unités : Cet invariant opératoire rend compte de la conversion des unités de numération entre elles, qu’elles soient adjacentes ou non, mais sans passage à l’unité simple (Exemple : 1 millier = 100 dizaines sans qu’il s’agisse du résumé de la procédure qui consiste à convertir 1 millier en 1000 unités puis à utiliser la conversion 10 unités = 1 dizaine pour obtenir 1000/10 = 100 dizaines)

Conversion avec retenue : Cet invariant opératoire rend compte du fait que lorsqu’il est nécessaire d’additionner au sein d’une unité de numération et que le résultat fait apparaître un nombre supérieur à 9, alors la conversion vers l’unité de numération supérieure est réalisée (Exemple : 8 dizaines et 3 dizaines cela fait 11 dizaines, donc 1 centaine et 1 dizaine).

Figure 1 – Six invariants opératoires identifiés dans les procédures des élèves et retenus pour modéliser les conceptions. la mise en œuvre est pertinente pour atteindre la réponse correcte, à gauche, les invariants opératoires relevant du principe de position, à droite, ceux relevant du principe décimal

Notre hypothèse est que les conceptions permettant d’expliquer la plupart des réponses des élèves dans les problèmes de numération sont principalement : une conception « position » qui inclut uniquement les invariants opératoires rattachés au principe de position et une conception retour à l’unité qui utilise essentiellement l’invariant opératoire retour à l’unité.

Les nouveaux invariants opératoires

Il est très intéressant de noter la grande variété des réponses incorrectes fournies par les élèves. Si 5 ou 6 réponses incorrectes représentent près de 50% des réponses incorrectes données par les élèves pour chaque exercice, il reste un nombre très important de réponses incorrectes différentes, d’une soixantaine de réponses différentes pour les exercices 2 ou 4 à 160 réponses incorrectes différentes données pour l’exercice 5 ! Le nombre de réponses incorrectes pour les exercices 1 à 7 est respectivement de 72, 66, 71, 65, 160, 137, 108. L’enjeu didactique est d’identifier parmi ces réponses celles qui sont le résultat de la mise en œuvre de l’un ou l’autre des deux principes de la numération (c’est-à-dire satisfaisant à l’un ou plusieurs des critères présentés ci-dessus) permettant de mesurer les apprentissages y compris dans les réponses erronées. Ce type d’analyse doit encore être conduit.

Au cours de ce travail d’analyse, il est apparu que d’autres invariants opératoires intervenaient et pouvaient être mis en oeuvre dans certaines réponses sans toutefois conduire à une réponse correcte, ou dans certains cas seulement. Même si un grand nombre de réponses incorrectes restent encore inexplicables, un certain nombre peut s’expliquer par la mise en oeuvre de l’un ou l’autre de ces invariants opératoires présentés ci-après, voire une combinaison de plusieurs d’entre-eux, conduisant à des réponses incorrectes.

Unité de numération décalée à droite : « Le chiffre le plus à gauche devient unité de l’UN considérée (sauf pour les unités) » Cet invariant opératoire se manifeste lorsque le chiffre le plus à gauche d’une unité de numération considérée, outre les unités, devient le chiffre des unités de cette unité de numération. (Exemple : 52 centaines = 5 centaines + 2 dizaines). Cet invariant opératoire est efficace lorsque chaque unité de numération ne contient que des nombres à un chiffre mais devient infructueux si une ou plusieurs unités de numération contiennent un nombre à au moins deux chiffres.

Somme des nombres : Cet invariant opératoire se manifeste lorsque les nombres de l’énoncé sont ajoutés sans la prise en compte des unités de numération. Chaque nombre est considéré comme unités. Par exemple, 15 centaines, 8 dizaines et 6 unités deviennent 29.

Ordre inversé : Cet invariant opératoire se manifeste lorsque les unités de numération sont positionnées dans l’ordre inverse de l’ordre conventionnel. Tout comme sur une droite numérique, le chiffre le plus à gauche est le plus petit. Par exemple, 3 centaines et 5 unités deviennent 503.

Juxtaposition des unités de numération : Cet invariant opératoire se manifeste lorsque les nombres des unités de numération, qu’ils viennent de l’énoncé ou qu’ils soient obtenus par addition dans leur propre unité de numération, sont juxtaposés sans conversion entre unités de numération, dans l’ordre de l’énoncé ou pas. Par exemple, 8 milliers, 52 centaines, 31 dizaines et 9 unités deviennent 852 319. ou Exemple : cf livret n°……..

Traitement des unités de numération dans l’ordre de l’énoncé : Cet invariant opératoire se manifeste lorsque les nombres de l’énoncé ne sont pas dans l’ordre des unités de numération et qu’ils sont traités comme s’ils étaient dans le bon ordre, sans la prise en compte de leur unité de numération respective. Exemple : 12 unités, 20 milliers et 7 dizaines deviennent 12 207

Prise en compte partielle ou erronée des données de l’énoncé : Cet invariant opératoire se manifeste lorsque les unités d’une classe sont considérées comme des unités simples. Par exemple, 53 unités de mille qui deviennent 53 unités simples.

Conclusion

Pour rendre opérationnelle l’analyse didactique des connaissances des élèves en numération décimale de position, nous avons choisi d’identifier ce que savent les élèves quand bien même leurs réponses ne sont pas correctes. Pour cela, nous avons défini des invariants opératoires identifiables dans les stratégies de résolution des élèves pour rendre opérationnelle l’analyse des connaissances des élèves en numération, en terme de principe de position et de principe décimal. Pour le principe de position, nous avons distingué trois types d’invariants opératoires qui permettent de repérer la façon dont les élèves savent gérer l’ordre des unités de numération et les zéros, qu’ils soient à droite aux unités et dizaines ou intercalés entre d’autres unités de numération. Pour le principe décimal, les trois invariants opératoires que nous avons défini caractérisent les connaissances des élèves sur les conversions : retour à l’unité, conversion entre unités et conversion avec retenue. A l’aide de ces invariants opératoires, nous avons pu analyser les principales stratégies de résolution des élèves, à partir de l’observation des résolutions ou bien des réponses finales.

Stratégies, invariants opératoires et conceptions relatives à la numération décimale de position

Malgré les nombreuses erreurs, la stratégie de retour à l’unité, qui consiste à transformer toutes les informations en unités simples puis à additionner, est résistante. Les élèves n’éprouvent pas le besoin de remplacer cette stratégie, rassurante, par une stratégie plus générale qui serait plus efficace sur les grands nombres et valide sur les décimaux. Une des limites de l’expérimentation est sûrement de n’avoir pas mesuré l’évolution des conceptions de la numération décimale avec les nombres décimaux.

Nous proposons de distinguer chez les élèves trois conceptions relatives à la numération décimale de position, selon qu’elles incluent ou pas certains de ces invariants opératoires. La conception « position » n’inclut que les trois invariants relatifs à la position, la conception « retour à l’unité » n’inclut que l’invariant retour à l’unité et la conception « décimale » inclut quatre invariants opératoires, les trois relatifs à la position et l’invariant conversion entre unités (qui permet aussi la conversion à l’unité simple).

La conduite de l’analyse nous amène à faire plusieurs remarques à propos des invariants opératoires et à énoncer une hypothèse. Nous avons identifié six invariants opératoires distincts, car directement liés aux principes de la numération. Mais les stratégies et les réponses des élèves pourraient être mieux modélisés en enrichissant cette première liste. Par exemple, décaler les unités de numération à droite, sommer les nombres disponibles, inverser les unités de numération ou juxtaposer chiffres ou nombres sont des éléments observés dans les stratégies de résolution des problèmes de numération qui pourraient générer des invariants opératoires et enrichir les conceptions déjà identifiées ou en caractériser d’autres. Par ailleurs, les invariants opératoires liés au principe position sont plus travaillés dans les classes peut être parce qu’ils sont plus facile à observer, en particulier dans la réponse finale des élèves. Nous nous sommes rendus compte qu’ils ne nécessitent pas d’observer toute la procédure pour pouvoir être identifiés, contrairement aux invariants opératoires du principe décimal.

Enfin, nous voulons conclure sur le décalage entre le ressenti positif des enseignants et l’évolution des conceptions des élèves mesurée expérimentalement. Les enseignants, sont bien plus positifs sur les progrès de leurs élèves que ce que montre l’expérimentation. Cela suscite des questions : les exercices des diagnostics ont-ils mesuré effectivement les apprentissages des élèves en numération ? Les progrès d’un quart ou un tiers des élèves est-il décevant expérimentalement et pourtant très significatif pour les enseignants ? Au delà des résultats, les enseignants sont positifs sur les apports de l’expérimentation. Ils évoquent une dynamique de travail différente, des élèves qui osent davantage produire une réponse, éléments non mesurés par les diagnostics en place. Ils témoignent du fait que le jeu a transformé le tableau de numération en un outil de numération, utilisé comme un outil pour résoudre des problèmes, en suivant des règles pour leur nécessité mathématique et pragmatique et non pour respecter des injonctions arbitraires. Les enseignants évoquent également dans leur grande majorité une évolution de leurs pratiques consécutive à la prise de conscience que le jeu a provoqué chez eux.